n these days of lockdown where we all have a lot more time on our hands than usual, you may have started to get a little bored. Well, one surefire way to outlast the lockdown would be to try your hand at solving some of the most complex math problems that have yet to be solved.

“DO NOT WORRY ABOUT YOUR DIFFICULTIES IN MATHEMATICS, I CAN ASSURE YOU THAT MINE ARE GREATER”Albert Einstein, Theoretical Physicist
As some of these have gone unsolved for hundreds of years, they should keep you plenty busy until some semblance of normality returns.
The Collatz Conjecture
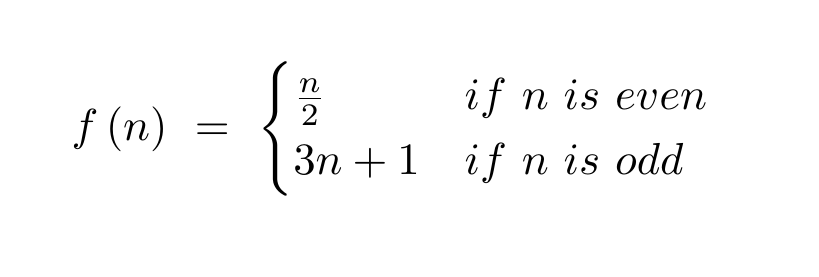
This is one of the complex math problems that has been baffling mathematicians for over 80 years. A prolific mind in this field, Terrence Tao, recently made giant leaps in solving the problem, but he admits his work is not quite there and it could be decades more until it’s complete.
In Collatz’s Conjecture, it’s all about the function f(n). It takes even numbers and cuts them in half. Odd numbers get tripled and then added to 1. It should follow then that if you take any natural number, apply f, then apply f again and again that you will eventually land on 1.
The conjecture is that this is true for all natural numbers and it relates to a discipline known as Dynamical Systems; the study of situations that change over time in predictable ways.
Even to a layperson this problem may appear an innocuous one but that’s what makes it so intriguing; why is such a basic question so hard to answer?
The Kissing Number Problem
This epic head-scratcher is connected to an area of math which is called Sphere Packing. And it is all about the stacking of spheres in any given space.
When spheres are packed together each has a kissing number. This is the number of other spheres that it is touching. If the sphere is touching 5 other spheres, it’s kissing number is 5. Essy enough for now.

The complex math problem arises when we start to talk about dimensions. A 1-d dimension is simply a straight line, so you know the kissing number for this dimension can be no more than 2. One to the left and one to the right.
2-d starts to incorporate the possibility of a plane and the boffins have this one well covered.
All the possibilities for 3d have also been worked out but they didn’t get there until the 1950s. And this was after it famously caused an argument between Sir Isaac Newtown and a colleague. Newton believed the answer was 12, his colleague said 13. He didn’t live long enough to hear the proof, but Newton was right.

So for the top minds have worked out the kissing number up to 24 dimensions, there is a long way for this very complex problem to be solved yet.
Goldbach’s Conjecture
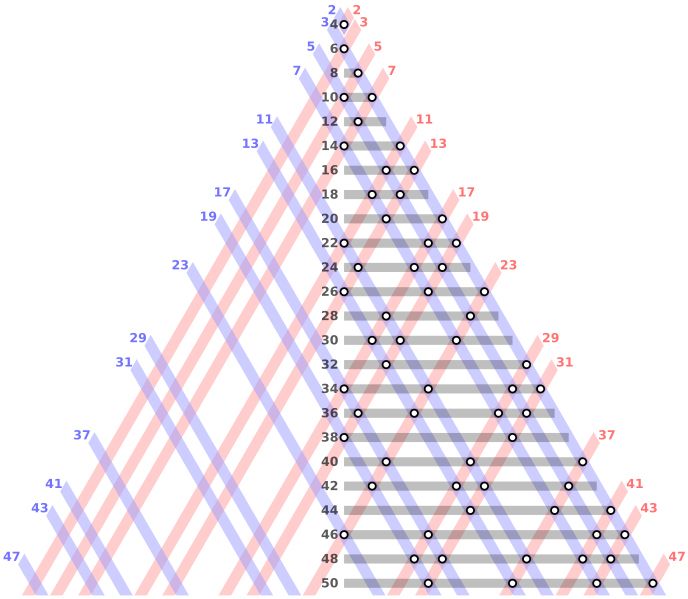
Another very simple premise which some could say means that these mad mathematical geniuses just like making things too complicated.
The question: Is every even number greater than 2 the sum of two primes?
For example, 3 + 1 = 4, 5 + 1 = 6, etc, etc.
The answer would seem to be a resounding yes. The problem is that you can keep counting for a very long time.
What if at some point some incredibly large number doesn’t follow the rule? Theoretically, it could be possible to find one that isn’t the sum of two primes.
As this number has not been reached yet, despite decades of counting, the search for this potential super number that might defy logic goes on.

















